Kalman滤波详解

1. 引言

在我们使用像超声波、红外测距、激光雷达等 “离散型” 数据传感器时，所得到的传感器数据会因为噪声的影响，使得发送出的数据在实际数据上下波动，如：

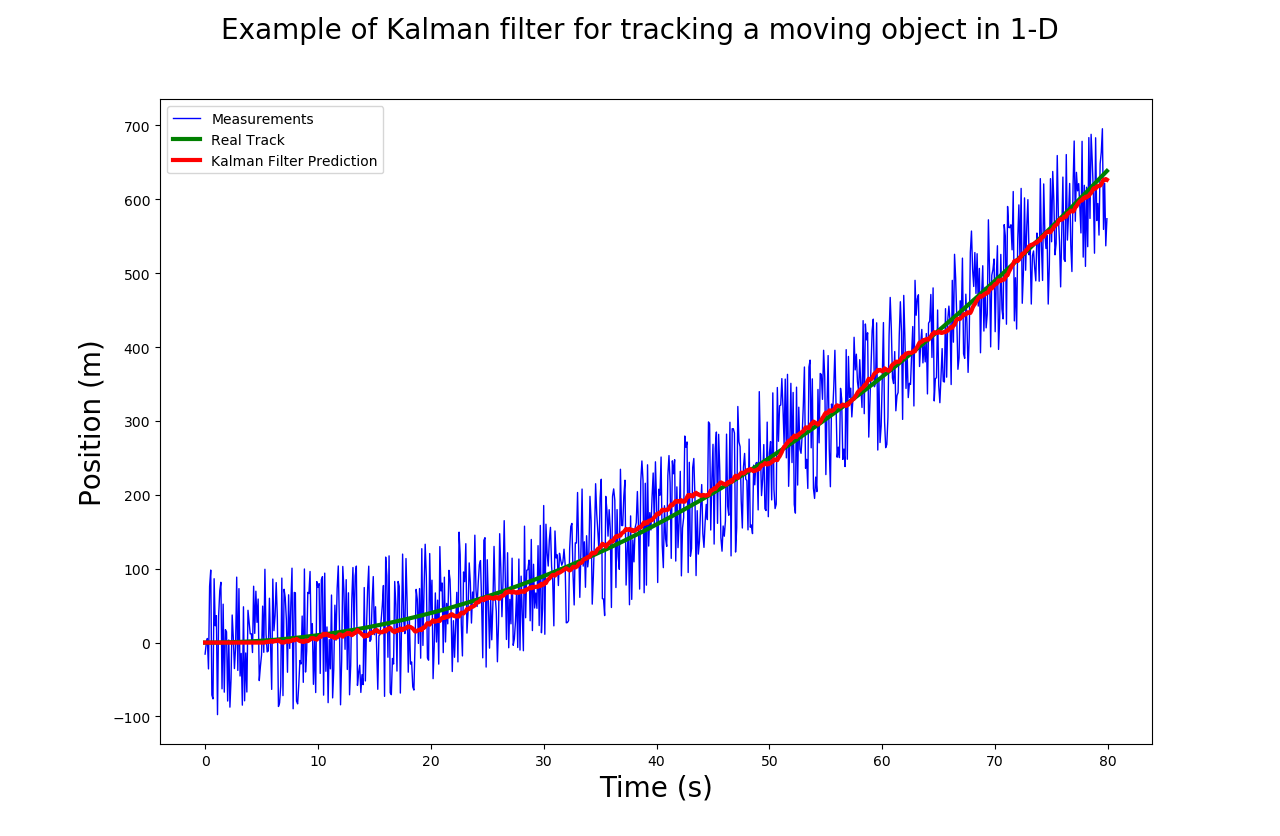
• 而卡尔曼滤波器用于估计系统状态，其利用系统的动态模型和传感器提供的观测值来更新对系统状态的估计，以得到最佳数据。

对于Kalman滤波器，其特点：

• 将系统状态建模为一个线性动态系统，
• 并假设系统的状态和观测值都受到高斯噪声的影响，
• 通过递归地更新两个步骤来实现状态估计：预测步骤、更新步骤。

其适用范围：

• 线性高斯系统，线性：满足叠加性和齐次性，高斯：噪声服从正态分布。

---

2. 进阶

2.1 状态空间

以下方程针对的是离散线性动态系统。

• 状态方程为：

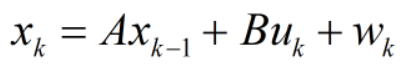
其中，

• Xk：当前状态值。

• AXk-1：Xk-1，上一状态值，A，权值。

• BUk：Uk，当前输入值，B：权值。

• Wk：过程噪声。

• ==当X为一维数组时，A=1。==

• 观测方程为：

其中，

• zk：观测值。

• HXk：同上。

• vk：测量噪声，其可能来自传感器自身误差。

• wk是按照理论计算出来的值但是跟实际有出入，这个误差可能来自过程中我们没考虑到的因素，不在我们的数学模型中，

• vk则是由于测量设备自身存在的误差，我们在使用时是将其理想化使用了的，例如GPS位置就有一个误差值。

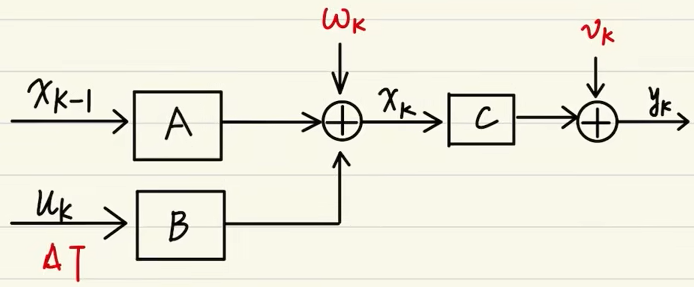
逻辑框图：

---

2.2 参数解析

对于wk和vk，其均满足正态分布，且 μ =0，我们统称其为：高斯白噪声。

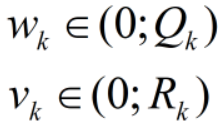
• 其中，Qk和Rk都是经常使用到的，且跟PID一样都需要实验训练得到，即超参数。

• kalman直观图解：

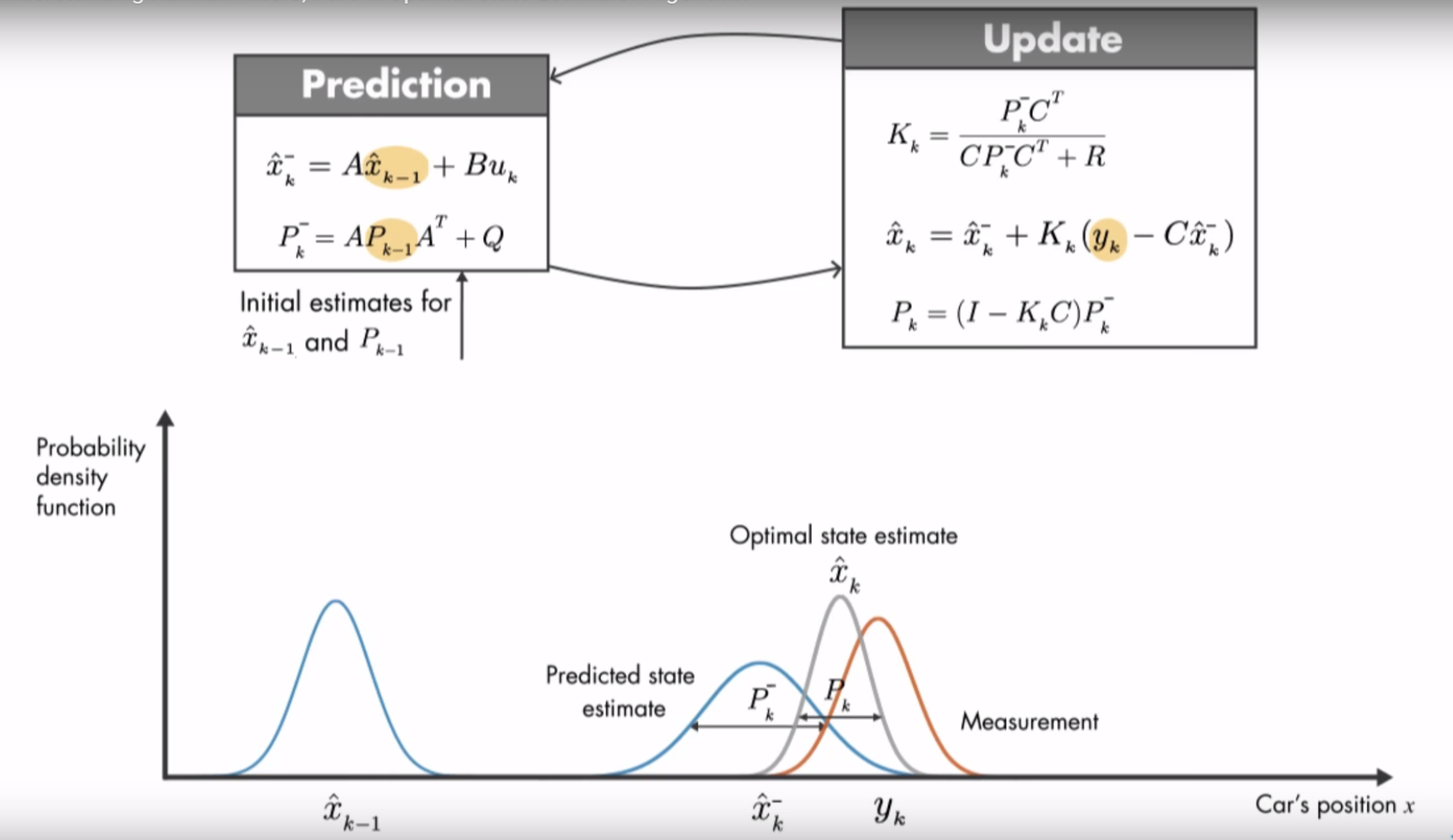
• 简单解释一下：Xk-1为上一次滤波结果，通过其得到Xk-，为先验状态估计值，而yk为测量值，将两者进行数据融合，得到Xk，即当前最优估计值。

---

3. 难点

• 上面我们已经分析了离散线性动态系统的状态方程和预测方程，而对于状态估计算法，我们可以利用，

• 以下针对以上三个状态矩阵进行分析。

3.1 Kalman推导

• 实现过程：使用上一次的最优结果预测当前值，同时使用预测值修正当前值。
• 书接上回，Kalman滤波分为：预测、更新。

3.1.1 状态估计协方差Pk

• 先验估计：由预测方程可知，得到预测值，==黄金第一法则==，

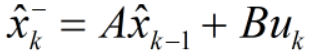
• 后验估计：由观测方程可知，得到最优估计值（最终结果），==黄金第二法则==，

其中，尤其值得注意的是K，称为卡尔曼增益：表征了模型预测误差与测量误差的比重，如下，

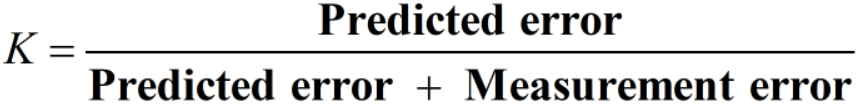
• 由此可以得到：

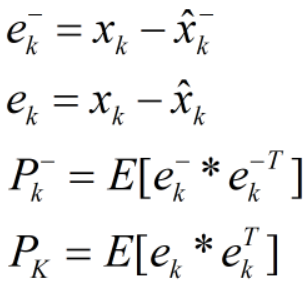
• 详解：
  • 1：先验状态误差
  • 2：后验状态误差
  • 3：真实值和预测值的协方差
  • 4：真实值与最优估计值的协方差

联立黄金第二法则和观测方程消去Zk，可知：

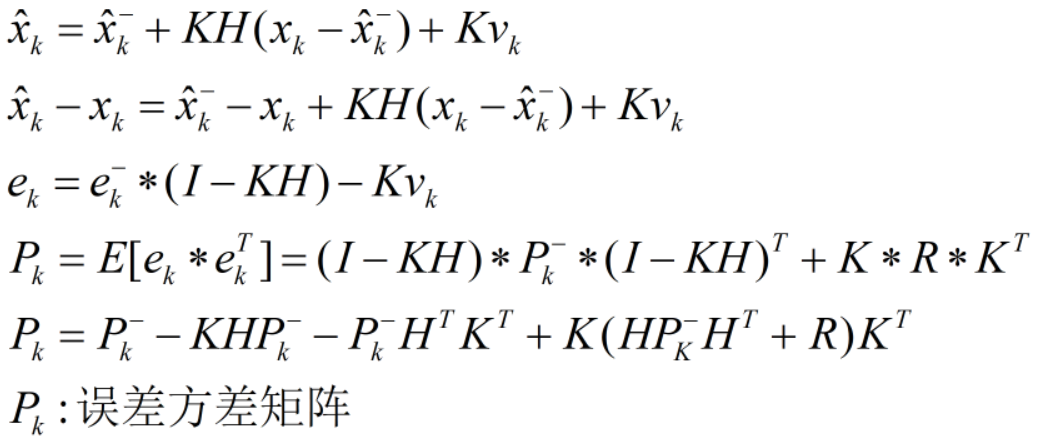
• 值得一提的是，随机变量跟自身的协方差为：方差。

3.1.2 状态变量（更新）

Kalman滤波的估计原则就是：使得状态估计协方差矩阵Pk的 ==“迹”== 最小，让其逼近真实值即：

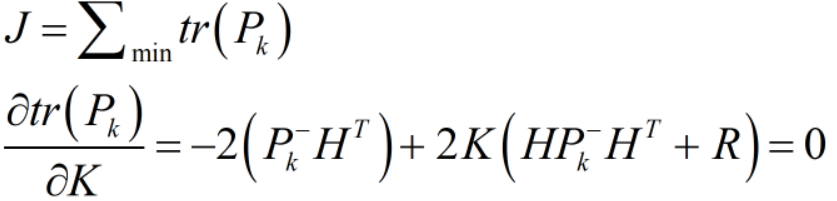
然后可以得到，最优估计条件下的卡尔曼增益矩阵，==黄金第三法则==：

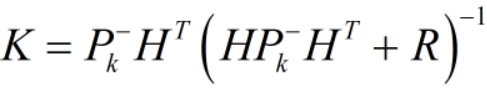
• 当**PK-**为一维数组时，H为1。

其次，可以得到估计误差方差矩阵，==黄金第四法则==：

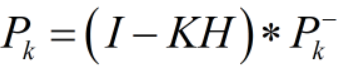
最后，可以得到预测估计协方差，==黄金第五法则==：

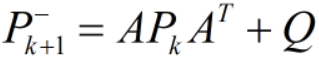
• 预测：

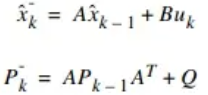
• 更新：

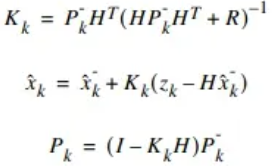
3.2 超参数推导

• …

---

4. C语言实现

• 可能大家对其还不是很清楚，但是没事 ”实践见真知！“
• 下面使用C语言进行实现，

参数	类型	含义
Last_p	float	上次估算协方差
Now_P	float	当前估算协方差
out	float	Kalman滤波输出最优值
kg	float	卡尔曼增益
Q	float	过程噪声协方差
R	float	观测噪声协方差

C语言如下：

#include<stdio.h>

//kalman参数结构体
typedef struct 
{
    float LastP;// 上次估算协方差 初始化值为0.02
    float Now_P;// 当前估算协方差 初始化值为0
    float out;// 卡尔曼滤波器输出 初始化值为0
    float Kg;// 卡尔曼增益 初始化值为0
    float Q;// 过程噪声协方差 初始化值为0.001
    float R;// 观测噪声协方差 初始化值为0.543
}KFP; // Kalman Filter parameter

//以高度为例,定义卡尔曼结构体并初始化参数
KFP KFP_height={0.02,0,0,0,0.001,0.543};

/**
 *卡尔曼滤波器
 *@param：
 *   KFP *kfp 卡尔曼结构体参数
 *   float input 需要滤波的参数的测量值（即传感器的采集值）
 *@return 滤波后的参数（最优值）
 */
 float kalmanFilter(KFP *kfp,float input)
 {
     //黄金第五法则，预测协方差方程：k时刻系统估算协方差 = k-1时刻的系统协方差 + 过程噪声协方差
     kfp->Now_P = kfp->LastP + kfp->Q;		// 由于此处输入x为一维，则系数A为1
     //黄金第三法则，卡尔曼增益方程：卡尔曼增益 = k时刻系统估算协方差 / （k时刻系统估算协方差 + 观测噪声协方差）
     kfp->Kg = kfp->Now_P / (kfp->Now_P + kfp->R);	// 由于此处Now_P为一维，故H=1
     //黄金第二、一法则，更新最优值方程：k时刻状态变量的最优值 = 状态变量的预测值 + 卡尔曼增益 * （测量值 - 状态变量的预测值）
     kfp->out = kfp->out + kfp->Kg * (input -kfp->out);// 因为这一次的预测值就是上一次的输出值
     //黄金第四法则，更新协方差方程: 本次的系统协方差付给 kfp->LastP 为下一次运算准备。
     kfp->LastP = (1-kfp->Kg) * kfp->Now_P;
     return kfp->out;
 }

int main(void){
    //调用滤波器，实践
    float height;
    height=xxxxx;   // 传感器数据
    float kalman_height=0;	 // 滤波结果
    kalman_height = kalmanFilter(&KFP_height,height);
    printf("输出：%.2f,\n",kalman_height);
    return 0;
}

---

5. 扩展卡尔曼滤波ROS实现

5.1 imu_gps_localization包

该项目（ROS包）是：利用EKF（扩展卡尔曼滤波）实现IMU与GPS信号的融合。

为什么要进行融合呢？

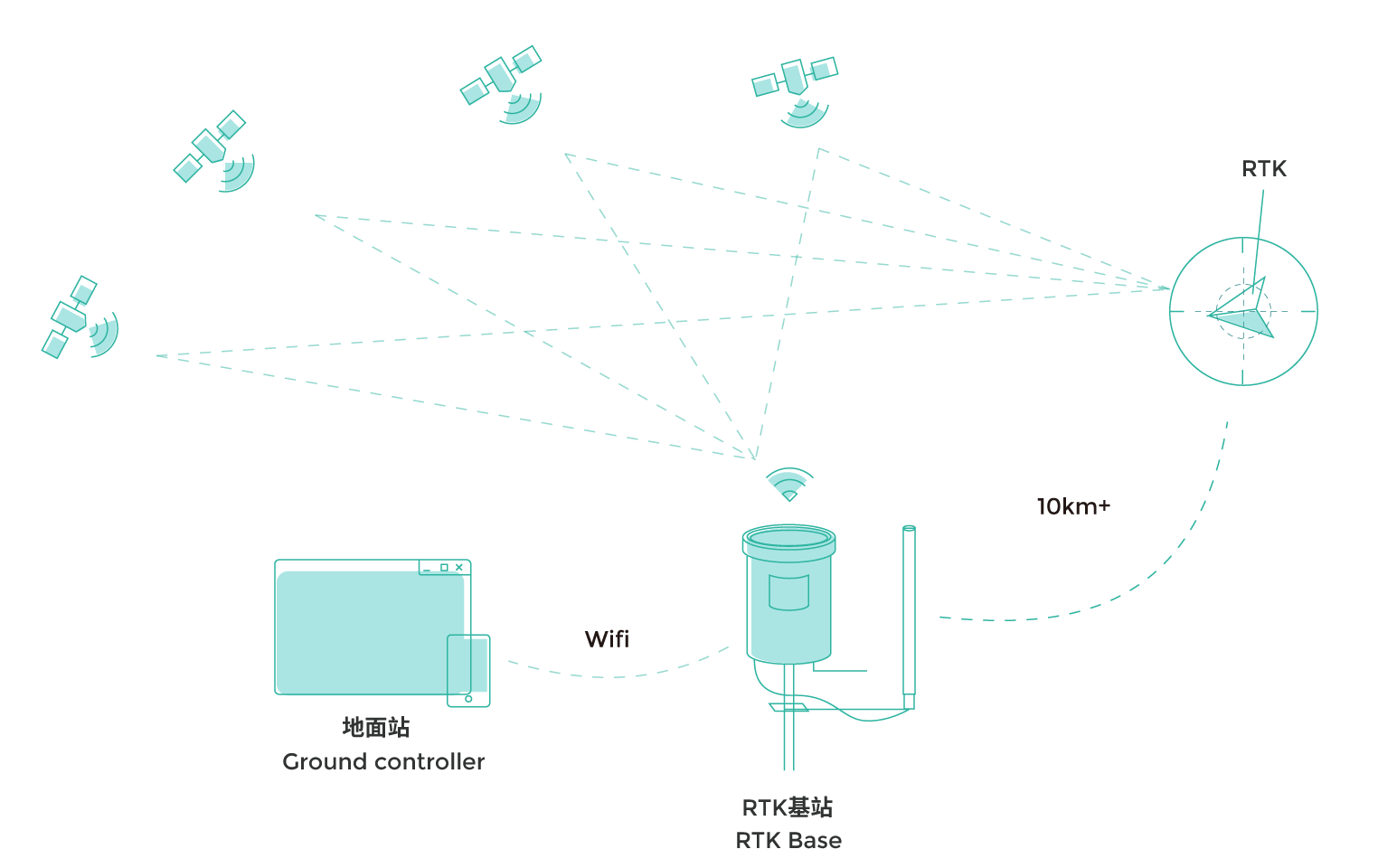
• IMU数据具有：高频率、灵敏，能有效提供姿态变化，但存在漂移等问题。
• GPS数据具有：位置精度高（RTK 厘米级误差）、可靠，但存在更新频率慢。

综上所述，仅仅使用GPS进行对车辆的完全控制显然是不可靠的。

下载包后，分析项目结构有：

├─doc ## 存放地图信息
├─imu_gps_localizer ## imu、GPS融合算法
│  ├─include
│  │  └─imu_gps_localizer
│  ├─src
│  └─third_party
│      └─GeographicLib ## 几何库
│          ├─include
│          └─src
└─ros_wrapper ## 封装
    ├─include
    ├─launch
    ├─rviz
    └─src

进入ros_wrapper目录中，首先观察启动文件的设计：

<launch>
    <param name="acc_noise"       type="double" value="1e-2" />
    <param name="gyro_noise"      type="double" value="1e-4" />
    <param name="acc_bias_noise"  type="double" value="1e-6" />
    <param name="gyro_bias_noise" type="double" value="1e-8" /> // imu噪声

    <param name="I_p_Gps_x"       type="double" value="0.0" />
    <param name="I_p_Gps_y"       type="double" value="0.0" />
    <param name="I_p_Gps_z"       type="double" value="0.0" /> // GPS在IMU坐标系下的位置

    <param name="log_folder"      type="string" value="$(find imu_gps_localization)" /> // 日志目录

    <node name="nmea_topic_driver" pkg="nmea_navsat_driver" type="nmea_topic_driver" output="screen" /> // nmea驱动
    <node name="imu_gps_localization_node" pkg="imu_gps_localization" type="imu_gps_localization_node" output="screen" /> // 融合

    <node pkg="rviz" type="rviz" name="rviz" output="screen"
      args="-d $(find imu_gps_localization)/ros_wrapper/rviz/default.rviz" required="true"> // 打开rviz配置，失败关闭整个进程
    </node>

</launch>

综上所述，只需在新建的work_ws/src下，添加imu_gps_localization和nmea_navsat_driver包进行编译即可。

而对于nmea_navsat_driver包的使用，其launch文件：

<launch>
    
  <arg name="port" default="/dev/ttyUSB0" />
  <arg name="baud" default="4800" />
  <arg name="frame_id" default="gps" />
  <arg name="use_GNSS_time" default="False" />
  <arg name="time_ref_source" default="gps" />
  <arg name="useRMC" default="False" />

  <node name="nmea_serial_driver_node" pkg="nmea_navsat_driver" type="nmea_serial_driver" output="screen">
    <param name="port" value="$(arg port)"/>
    <param name="baud" value="$(arg baud)" />
    <param name="frame_id" value="$(arg frame_id)" />
    <param name="use_GNSS_time" value="$(arg use_GNSS_time)" />
    <param name="time_ref_source" value="$(arg time_ref_source)" />
    <param name="useRMC" value="$(arg useRMC)" />
  </node>

</launch>

• 发布的ROS话题：启动 nmea_navsat_driver 后，它会解析 NMEA 数据并发布以下 ROS 话题：

  • /fix：标准的 sensor_msgs/NavSatFix 消息，包含位置信息。

  • /vel：标准的 geometry_msgs/TwistStamped 消息，包含速度信息（如果可用）。

  • /time_reference：标准的 sensor_msgs/TimeReference 消息，包含时间参考信息（如果可用）。

则通过以上文件的配置，我们就可以实现imu与GPS信号的融合，完整完整操作为：

sudo chmod 666 /dev/ttyUSB0
roscore
roslaunch imu_gps_localization imu_gps_localization.launch 

值得注意的是：该项目需要自己设计imu话题发布对象，话题名：/imu/data，为标准sensor_msgs格式。